Buku Sistem Elektronik ( BSE ) IPA SMP Kelas 9

IPA SMP Kelas 9 Contextual Teaching - Nur Kuswanti Dkk

Baca Selengkapnya

Buku Sistem Elektronik ( BSE ) IPA SMP Kelas 9

IPA SMP Kelas 9 MariBelajar Ilmu Alam Sekitar - Sukis Wariyono Dkk

Baca Selengkapnya

Buku Sistem Elektronik ( BSE ) IPA SMP Kelas 9

IPA SMP Kelas 9 MariBelajar IPA - Elok Sudibyo Dkk

Baca Selengkapnya

Buku Sistem Elektronik ( BSE ) IPA SMP Kelas 9

IPA SMP Kelas 9 Pembelajaran IPA Terpadu Dan Kontekstual - Dewi Ganawati Dkk

Baca Selengkapnya

Buku Sistem Elektronik ( BSE ) IPA Kelas VIII - Agus Krisno

IPA SMP Kelas 8 - AgusKrisno Dkk

Baca Selengkapnya

Buku Sistem Elektronik ( BSE ) IPA Kelas VIII - Saeful Karim Dkk

Belajar IPA Membuka Cakrawala Sekitar SMP Kelas 8 - Saeful Karim Dkk

Baca Selengkapnya

Buku Sistem Elektronik IPA Terpadu Kelas VII - Anni Winarsih Dkk

IPA Terpadu SMP Kelas VII-Anni Winarsih

Baca Selengkapnya

Buku Sistem Elektronik IPA Kelas VII - Teguh

Ipa Smp Kelas Vii-teguh

Baca Selengkapnya

Buku Sistem Elektronik IPA Kelas VII-Wasis

IPA SMP Kelas 7- Wasis

Baca Selengkapnya

Menentukan ukuran kekuatan lensa kaca mata pada cacat mata

Fungsi mata manusia adalah untuk melihat. Mata bisa melihat dengan jelas apabila ada berkas cahaya yang dipantulkan benda masuk ke mata. Lensa mata berfungsi membentuk bayangan yang terbalik dengan bendanya. Lensa mata normal mempunyai kemampuan untuk mencembung dan memipih sesuai dengan jarak benda yang disebut daya akomodasi. Bayangan yang terbentuk harus tepat jatuh di retina. Retina adalah bagian mata yang peka terhadap cahaya dan berfungsi sebagai penangkap bayangan. Bayang yang terbalik akan ditegakkan kembali oleh syaraf mata sebelum sinyalnya diteruskan ke otak. Bagaimanakah bila bayangan tidak tepat jatuh di retina ? Bila bayangan jatuh di depan atau di belakang retina maka mata tersebut dikatakan mengalami cacat mata.

a. Mata Miopi (Rabun Jauh)

Cacat mata ini terjadi apabila mata melihat benda pada jarak yang jauh bayangan yang terbentuk jatuh di depan retina. Hal ini terjadi karena lensa mata tidak mampu memipih sesuai jarak benda. Sebab terjadinya cacat mata miopi dikarenakan kebiasaan melihat jarak dekat yang terlalu lama, sehingga lensa mata terbiasa berakomodasi atau mencembung dan pada saat melihat benda yang jauh lensa mata tidak bisa memipih sebagaimana mestinya. Contoh kebiasaan membaca yang terlalu dekat dengan mata dan dalam waktu yang lama. Perhatikan gambar berikut:

Mata Miopi

Cacat mata miopi ditolong dengan kaca mata berlensa cekung atau negatif (-)
Kaca mata negatif berfungsi mengubah jarak benda yang jauh (So=∼) sehingga mendekat tepat pada titik jauh mata/punctum remotum (Si=-PR), harga negatif ini karena sifat bayangan maya.
Ukuran kaca mata ditentukan dengan kekuatan lensa dengan satuan dioptri
Rumus :
P = 1/f   (jika dalam satuan m) → P = -1/PR (dioptri)
P = 100/f (jika dalam satuan cm) → P = - 100/-PR (dioptri)

Perhatikan gambar pembentukan bayangan yang dibentuk oleh kaca mata negatif !

b. Mata Hipermetropi (Rabun Dekat)

Cacat mata ini terjadi apabila mata melihat benda pada jarak baca normal bayangan yang terbentuk jatuh di belakang retina. Hal ini terjadi karena lensa mata tidak mampu berakomodasi atau mencembung sesuai jarak benda, sehingga titik dekat mata (punctum proximum) menjadi lebih jauh dari mata. Sebab terjadinya mata hipermetropi dikarenakan kebiasaan melihat benda yang jaraknya jauh, sehingga lensa mata terbiasa memipih dan pada saat melihat benda pada jarak baca normal lensa mata tidak mampu berakomodasi atau mencembung sebagaimana mestinya. Contoh orang pengamat yang menggunakan teropong. Perhatikan gambar berikut:

Mata Hipermetropi

Cacat mata hipermetropi ditolong dengan kaca mata berlensa cembung atau positif (+)
Kaca mata positif berfungsi mengubah jarak baca normal (So=25 cm) hingga menjauh dari mata tepat pada titik dekat mata/punctum proximum (Si=-PP), harga negatif ini karena sifat bayangan maya. Ukuran kaca mata ditentukan dengan kekuatan lensa dengan satuan dioptri. Karena PP> 25 cm maka kekuatan lensa selalu positif.
Rumus :
P = 1/f   (jika dalam satuan m) → P = 1/25 - 1/PP
P = 100/f (jika dalam satuan cm) → P = 100/25 - 100/PP = 4 - 100/PP

Perhatikan pembentukan bayangan yang dibentuk oleh kaca mata positif !

c. Mata Presbiopi (Miopi dan Hipermetropi) atau Cacat mata ganda

Cacat mata ini terjadi apabila mata tidak dapat melihat benda pada jarak yang jauh dan pada jarak baca normal karena bayangan benda yang jauh jatuh di depan retina sedang bayangan benda pada jarak baca normal jatuh di belakang retina. Hal ini terjadi karena lensa mata tidak mampu berakomodasi sesuai dengan jarak benda, sehingga titik jauh mata (punctum remotum) menjadi dekat dengan mata dan titik dekat mata (punctum proximum) menjadi lebih jauh dari mata. Sebab terjadinya mata presbiopi disebabkan karena penurunan fisik lensa mata karena usia tua. Perhatikan gambar berikut !

Mata tua / presbiopi

Cacat mata presbiopi ditolong dengan kaca mata ganda / rangkap yaitu kaca mata negatif dan kaca mata positif. Perhatikan gambar berikut !

Kaca mata presbiopi / lensa ganda

Soal 1 :

Seorang penderita rabun jauh / miopi hanya mampu melihat benda dengan jelas paling jauh 4 m dari matanya. Berapakah ukuran kekuatan lensa kaca mata yang diperlukannya ?

Pembahasan:

Untuk menentukan ukuran kekuatan lensa kaca mata miopi harus memperhatikan jarak benda yang mampu dilihat dengan jelas oleh mata dinamakan titik jauh (punctum remotum) (Si=-PR), sedangkan benda yang lebih jauh yang tidak dapat dilihat dengan jelas (So= ∼). Kekuatan lensa kaca matanya dirumuskan P= - 1/PR

Jawaban:

Diketahui:

So = ∼
Si  = PR = 4 m

Ditanyakan: P = ...?

Jawab:

P = -1/PR
P = - 1/4 dioptri
P = -  0.25 dioptri

Jadi ukuran kekuatan lensa kaca mata orang tersebut -0,25 dioptri

Soal 2 :

Seseorang penderita hipermetropi lupa membawa kacamata yang biasa digunakan untuk membaca koran sehingga saat itu dia membaca koran dengan diletakkan sedikit lebih jauh dari jarak baca normal yaitu 50 cm. Berapakah ukuran kekuatan lensa yang harus dipakai orang tersebut ?

Pembahasan:

Jarak baca normal orang adalah 25 cm yang disebut jarak benda (So). Titik dekat mata orang itu bergeser menjauh dari mata lebih dari jarak baca normal yang disebut (Si). Kekuatan lensa kaca mata ditentukan dengan rumus: P = 100/So - 100/Si atau P = 4 - 100/Si

Jawab:

Diketahui:

So = 25 cm
Si  = 50 cm

Ditanya: P = ... ?

Jawab:

P = 4 - 100/Si
P = 4 - 100/50
P = 4 - 2
P = 2 dioptri

Jadi ukuran kekuatan lensa kaca mata orang tersebut 2 dioptri

Baca Selengkapnya

Menentukan jarak fokus, jarak benda dan jarak bayangan pada cermin cekung

Cermin cekung adalah cermin yang berbentuk irisan bola yang bagian dalamnya memantulkan keseluruhan cahaya yang diterimanya. Cermin cekung disebut cermin konvergen karena bersifat mengumpulkan sinar-sinar pantul. Titik berkumpulnya sinar-sinar pantul dinamakan titik fokus atau titik api. Cermin cekung biasanya digunakan untuk mengarahkan cahaya agar berkas sinar pantulnya sejajar. Contohnya pada reflektor proyektor, lampu kendaraan dan lampu senter.

Cermin Konvergen

Sinar-sinar istimewa pada cermin cekung yaitu:

1. Berkas sinar datang yang sejajar sumbu utama dipantulkan melalui titik fokus.

2. Berkas sinar datang yang melalui titik fokus dipantulkan sejajar sumbu utama

3. Berkas sinar yang melalui titik pusat kelengkungan cermin dipantulkan kembali melalui titik itu juga.

Berikut bagian-bagian cermin cekung:

Keterangan:

M = Titik pusat kelengkungan cermin
F = Titik Fokus
O = Titik pusat bidang cermin
Garis yang melalui M-O = Sumbu utama cermin
M-O = Jari-jari kelengkungan cermin ( R )
F-O = Jarak fokus cermin ( f )
I = Ruang satu
II = Ruang dua
III = Ruang tiga
IV = Ruang empat

Rumus terbentuknya bayangan:

Jika benda di ruang I maka bayangan yang terbentuk di ruang IV
Ruang benda + Ruang bayangan = 5

Jika benda di runag II maka bayangan yang terbentu di ruang III
Ruang benda + Ruang bayangan = 5

Jika benda di runag III maka bayangan yang terbentuk di ruang II
Ruang benda + Ruang bayangan = 5

Rumus- rumus persamaan pada cermin cekung:

Soal 1 : (mencari jarak fokus)

Sebuah benda berdiri tegak di depan cermin cekung pada jarak 15 cm, jika bayangan yang terbentuk pada jarak 30 cm, maka berapakah jarak fokus cermin cekung tersebut ?

Jawaban:

Diketahui:
So = 15 cm
Si = 30 cm

Ditanya: f = ... ?

Jawab:

Jadi jarak fokus cermin cekung besarnya 10 cm


Soal 2 : (mencari jarak bayangan)

Sebuah benda terletak didepan cermin cekung yang mempunyai jarak fokus 15 cm. Jika jarak benda terhadap cermin cekung 20 cm, maka berapakah jarak bayangan yang terbentuk ?

Jawaban:

Diketahui:

So = 20 cm
f = 15 cm

Ditanya: Si = ... ?

Jawab:

Jadi jarak bayangan yang terbentuk besarnya 60 cm


Soal 3 : (mencari jarak benda)

Sebuah benda diletakkan di depan cermin cekung yang jarak fokusnya 20 cm. Jika bayangan yang terbentuk terletak pada jarak 30 cm, maka berapakah jarak antara benda terhadap cermin ?

Jawaban:

Diketahui:

f  = 20 cm
Si = 30 cm

Ditanya: So = ... ?

Jawab:

Jadi jarak antara benda terhadap cermin cekung adalah 60 cm

Baca Selengkapnya

Menghitung kecepatan akhir ( Vt ) pada gerak lurus berubah beraturan (GLBB)

Gerak Lurus (GL) adalah gerak suatu benda yang lintasannya menurut garis lurus.

Gerak Lurus Beraturan (GLB) adalah suatu gerak lurus yang mempunyai kecepatan konstan. Maka nilai percepatannya adalah a = 0. Gerakan GLB berbentuk linear dan nilai kecepatannya adalah hasil bagi jarak dengan waktu yang ditempuh.

Rumus:

Dengan ketentuan:

• = Jarak yang ditempuh (km, m)
• = Kecepatan (km/jam, m/s)
• = Waktu tempuh (jam, sekon)

Gerak lurus berubah beraturan (GLBB) adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.

Percepatannya bernilai konstan/tetap.
Rumus GLBB yaitu:

• 

• 

Dengan ketentuan:

• = Kecepatan awal (m/s)
• = Kecepatan akhir (m/s)
• = Percepatan (m/s²)
• = Jarak yang ditempuh (m)

 

Gerak Lurus Berubah Beraturan (GLBB) dipercepat, Contoh gerak benda yang jatuh bebas. Gerak jatuh bebas mengalami percepatan oleh gravitasi sehingga kecepatannya semakin besar.

Gerak Lurus Berubah Beraturan (GLBB) diperlambat, Contoh  gerak benda yang kita lempar vertikal ke atas.  Gerak vertikal ke atas mengalami perlambatan oleh gravitasi, karena itu kecepatannya semakin kecil.

Contoh Soal:

Sebuah mobil melaju dengan kecepatan awal 20 m/s, mobil tersebut dipercepat konstan setiap sekon menambah tambahan kecepatan 2 m/s. Berapakah kecepatan mobil tersebut setelah bergerak 20 sekon ?

Pembahasan:
Kecepatan awal mobil melaju adalah Vo, tambahan kecepatan setiap sekon adalah percepatan (a), lama waktu mobil melaju (t). Kecepatan akhir dari mobil melaju (Vt)

Jawaban:

Diketahui:

Vo = 20 m/s
a   = 2 m/s²
t   = 20 s

Ditanya: Vt = ....?

Jawab:

Vt  =  Vo  + at
      =  20 m/s + 2 m/s² . 20 s
      =  20 m/s + 40 m/s
      =  60 m/s

Jadi kecepatan akhir (Vt) mobil melaju selama 20 s adalah 60 m/s

Baca Selengkapnya

Menghitung gaya angkat alat pengangkat mobil hidrolik

Alat pengangkat mobil hidrolik biasanya diprgunakan pada bengkel mobil atau tempat cuci mobil. Alat ini dibuat dari dua tabung / bejana yang berbeda besarnya dan saling berhubungan, antara dua tabung disekat dan dipasangi katup. Masing-masing tabung dipasangi piston, tabung kecil untuk memompa sedangkan tabung besar untuk mengangkat mobil. Prinsip kerjanya sama dengan dongkrak hidrolik yaitu dengan dasar Hukum Pascal. Hukum Pascal berbunyi Tekanan yang diberikan pada zat cair dalam ruang tertutup akan diteruskan sama besar ke segala arah. Bagaimana menghitung besar gaya yang digunakan untuk mengangkat mobil ?

Contoh Soal:

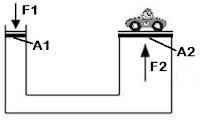
Perhatikan gambar berikut !

Alat pengangkat mobil hidrolik masing-masing tabung mempunyai piston A1 = 10 cm² dan A2 = 2.000 cm². Jika gaya F1 yang digunakan untuk memompa pada piston A1 besarnya 20 N, berapakah gaya F2 yang digunakan untuk mengangkat mobil ?

Pembahasan:

Hukum Pascal : Tekanan yang diberikan pada zat cair dalam ruang tertutup akan diteruskan sama besar ke segala arah.



Keterangan:

• F₁: Gaya tekan pada piston 1
• F₂: Gaya tekan pada piston 2
• A₁: Luas penampang pada piston 1
• A₂: Luas penampang pada piston 2

Tekanan yang diberikan pada tabung kecil sama dengan  tekanan yang ditimbulkan pada tabung besar

Jawaban:

Diketahui:

A1 = 10 cm²

A2 = 2.000 cm²

F1 = 20 N

Ditanya: F2 = ... ?

Jawab:

Jadi besar gaya F2 yang digunakan untuk mengangkat mobil adalah 4.000 N

Baca Selengkapnya

Menghitung rekening listrik selama 1 bulan

Penggunaan listrik setiap rumah yang berlangganan listrik dari PLN wajib harus dibayar, apabila tidak membayar resikonya akan diputus saluran listriknya. Berapa yang harus dibayar ? Kita harus tahu cara menghitungnya. Bagaiman cara menghitungnya ?

Contoh Soal:

Sebuah rumah berlangganan listrik dari PLN. Rumah tersebut menggunakan 4 lampu TL masing-masing  10 watt menyala 5 jam sehari, 1 buah TV 80 watt menyala 10 jam sehari, 2 buah kipas angin masing-masing 25 watt menyala 6 jam sehari, 1 buah kulkas 75 watt menyala 24 sehari dan 1 buah setrika 150 watt menyala 2 jam sehari. Jika harga 1 Kwh yang ditetapkan oleh PLN Rp 500,00 berapakah rekening yang harus dibayar selama 1 bulan ?

Pembahasan:

Rekening listrik yang harus dibayar oleh rumah yang berlangganan listrik dari PLN adalah besar energi listrik / daya listrik alat yang digunakan selama 1 bulan. Besar energi listrik dihitung sesuai tarip tiap Kwh. Perhitungan energi dilakukan dengan rumus persamaan berikut: W = P x t

Jawaban:

a. Energi listrik yang dipergunakan dalam 1 hari:

• 4 TL x 10 w x 5 h          =    200 wh   =  0,2 Kwh
• 1 TV x 80 w x 10 h       =     800  wh  =  0,8 Kwh
• 2 kipas x 25 w x 6 h      =     300 wh   =  0,3 Kwh
• 1 Kulkas x 75 w x 24 h =  1.800 wh   =  1,8 Kwh
• 1 Strk x 150 w x 2 h     =     300 wh   =  0,3 Kwh

Jumlah = 3,5 Kwh

b. Rekening listrik yang harus dibayar selama 1 bulan:

• 3,5 Kwh x Rp 500,00 x 30 hari = Rp 52.500,00

Jadi rekening listrik yang harus dibayar rumah yang berlangganan listrik selama 1 bulan besarnya Rp 52.500,00 ( ini belum termasuk biaya pajak penerangan jalan sebesar 9% dan biaya abunemen/ berlangganan)

Baca Selengkapnya

Menghitung tekanan hidrostatis

Contoh Soal:

Perhatikan gambar berikut ini !

 Jika gaya gravitasi ditempat itu sebesar 10 m/s², maka berapakah tekanan hidrostatis tepat di mulut ikan ?

Pembahasan:

Tekanan hidrostatis adalah tekanan yang ditimbulkan oleh zat cair yang kondisinya tenang. Tekanan hidrostatis ditentukan beberapa faktor yaitu massa jenis zat cair, gaya gravitasi ditempat itu dan kedalaman zat cair. Tekanan hidrostatis dapat dirumuskan dengan persamaan berikut:

Ph = ρ x g x h
Ph = h x s


Keterangan:

• Ph : Tekanan hidrostatis (N/m² atau dn/cm²)
• h   : jarak ke permukaan zat cair (m atau cm)
• s   : berat jenis zat cair (N/m³ atau dn/cm³)
• ρ  : massa jenis zat cair (kg/m³ atau g/cm³)
• g  : gravitasi (m/s² atau cm/s²)

Jawaban:

Diketahui:

h = 100 cm - 15 cm = 85 cm = 0,85 m
ρ = 1000 kg/m³
g = 10 m/s² 
  
Ditanya: Ph = .....?

Jawab:

Ph = ρ x g x h
Ph = 1000 kg/m³ x 10 m/s² x 0,85 m
Ph = 8.500 kg/m³s²
Ph = 8.500 N/m²
Ph = 8.500 pa

Jadi tekanan hidrostatis tepat pada mulut ikan besarnya 8.500 N/m² atau 8.500 pa

Baca Selengkapnya

Menghitung massa jenis benda yang bentuknya beraturan dan yang bentuknya tidak beraturan

Massa jenis adalah hasil bagi antara massa benda dengan volumenya. Massa jenis untuk benda yang jenisnya berbeda besarnya berbeda. Massa jenis dapat digunakan untuk menentukan jenis benda dengan membandingkan massa jenis yang telah diketahui. Perbandingan massa jenis benda yang berbeda dapat menjelaskan mengapa benda dapat terapung, melayang dan tenggelam jika salah satu benda dalam wujud cair. Massa jenis dirumuskan dengan persamaan sebagai berikut:

ρ = m / v

Keterangan :

• ρ = Massa jenis (kg/m³) atau (g/cm³)
• m = massa (kg atau gram)
• v = volume (m³ atau cm³)

a. Menghitung massa jenis benda yang bentuknya beraturan

Contoh soal:

Sebuah kubus tembaga dengan sisi 2 cm, setelah ditimbang dengan neraca massanya 200 gram. Berapakah massa jenis kubus tembaga tersebut ?

Pembahasan:
Kubus tembaga adalah benda yang bentuknya beraturan. Volume kubus dapat dihitung dengan mengalikan sisi-sisinya yaitu dengan rumus: V = sisi x sisi x sisi

Jawaban:

Diketahui:
sisi kubus = 2 cm
massa kubus = 200 gram

Ditanya: Massa Jenis = ... ?

Jawab:
V kubus = sisi x sisi x sisi
              = 2 cm x 2 cm x 2 cm
              = 8 cm³

b. Menghitung massa jenis benda yang bentuknya tidak beraturan


Contoh soal:

Perhatikan gambar berikut !

Jika massa benda yang dicelupkan ke dalam gelas ukur 100 gram, maka berapakah massa jenis benda tersebut ?

Pembahasan:
Untuk menghitung volume benda yang bentuknya tidak beraturan diperlukan gelas pengukur. Cara menggunakannya isi gelas pengukur dengan air, tinggi awal dibuat lebih rendah kira-kira 150 ml. kemudian benda dimasukkan ke dalam gelas, maka air dalam gelas akan terdesak sehingga naik lebih tinggi dari semula. kita lihat skala yang ditunjuk 200 ml. Skala akhir dikurangi skala awal itu menunjukkan volume benda.

Jawaban:
Diketahui:
m = 100 gram
V = 200 ml - 150 ml = 50 ml atau 50 cm³

Ditanyakan: Massa Jenis = ... ?

Jawab: 

Baca Selengkapnya